#100 Independence day, part 3

In posts #95 and #99 (here and here), I described examples that my students work through when we study the probability concept of independent events.  Now in part 3 of this series, I will describe three assessment items that I have used for this topic.  The first is a single question.  The second is a five-question, auto-graded quiz.  The third is a multi-part assignment.  In addition to giving students practice working with probabilities involving independent events, each of these assessments also aims to sneak in another topic from probability or statistics.

As always, questions that I pose to students appear in italics.

---

1. Suppose that a researcher conducts 20 independent tests, each of which has a 5% chance of resulting in an error.  Determine the probability that at least one of these tests results in an error.

This question is similar to the example (from post #95, here) involving a daily lottery number.  The solution is: Pr(at least one error) = 1 – Pr(no errors) = 1 – Pr(first test does not result in an error and second test does not result in an error and … and twentieth test does not result in an error) = 1 – (1 – 0.05)^20 = 1 – (0.95)^20 ≈ 0.642.

When I discuss this question in class, I point out that this calculation reveals a problem with conducting a large number of tests.  Even with a small probability of error on any one test, performing a large number of tests results in a substantial probability of committing at least one error.  This is a primary objection to the ill-advised practice sometimes known as p-hacking.  This xkcd cartoon (here) provides a wonderful illustration of p-hacking.

---

2. Suppose that the two sports teams, the Domestic Shorthairs and the Cache Cows, play a series of games.  Assume that the results of the games are independent and that the Domestic Shorthairs have a 0.6 probability of winning each game.

a) What does it mean to say that the results of the games are independent?  [Options: A) The probabilities of winning later games do not change, regardless of which team wins earlier games. B) Each team has a 50-50 chance to win each game. C) It’s impossible for the same team to win two games in a row. D) Whichever team wins a game has a larger probability of winning the next game. E) Whichever team wins a game has a smaller probability of winning the next game.]  The correct answer is A), but option B) can entice many students.

b) Determine the probability that the Domestic Shorthairs win the first two games of the series.  Applications of the multiplication rule for independent events do not come simpler than this.  If we let W denote a win and L a loss for the Domestic Shorthairs, this probability is calculated as: Pr(W1 and W2) = Pr(W1) × Pr(W2) = 0.6×0.6 = 0.36.

c) Determine the probability that the Domestic Shorthairs win two games before the Cache Cows win two games.  This question is somewhat similar to “unfinished game” example from post #99, here.  This probability can be calculated as: Pr[(W1 and W2) or (W1 and L2 and W3) or (L1 and W2 and W3)] = 0.6×0.6 + 0.6×0.4×0.6 + 0.4×0.6×0.6 = 0.648.  When I present this as an in-class example rather than an out-of-class assessment, I first ask students to predict, without performing calculations, whether the answer will be equal to 0.6, less than 0.6, or greater than 0.6.

d) Suppose that the Domestic Shorthairs’ probability of winning each game was larger than 0.6.  How would this change the probability that the Domestic Shorthairs win two games before the Cache Cows win two games?  [Options: A. No change, B) Increase, C) Decrease]  This question is meant to be quite easy: A larger probability of winning any one game also leads to a larger probability of winning the series, so the correct option is B).

e) Now suppose that you are a fan of the Domestic Shorthairs and want them to win the series of games against the Cache Cows.  Assume again that the Domestic Shorthairs have a 0.6 probability of winning any one game and that game results are independent from game to game.  Would you prefer them to play a single game, a best-of-three series, or a best-of-five series?  [Options: A) Single game, B) Best-of-three, C) Best-of-five, D) No preference]  The correct answer here is C).  A longer series favors the stronger team.  From the opposite perspective, the underdog would prefer to play a single game rather than a longer series, in which the better team is more likely to demonstrate its superiority.  This question sneaks in the idea that a larger sample size is more likely to produce a sample result similar to the truth about the population.  If this were not an auto-graded quiz, I would ask students to explain their answer for part (e).

---

The next question is a fairly long assignment with ten parts.  This assignment introduces students to connections in series and connections in parallel.  Most of these parts ask typical questions, so you might want to skip ahead to the more interesting parts (i) and especially (j). 

3. Consider a system that requires all components to function successfully in order for the system to function successfully.  (Such a system is said to be connected in series.)  Suppose that the components operate independently and that the probability that a single component functions successfully is 0.95.

• a) Determine the probability that a system with two components connected in series functions successfully.  Also indicate the probability rule(s) that you use for this calculation.
• b) Now suppose that the system consists of three components connected in series.  Determine the probability that this system functions successfully.  Is this probability larger, smaller, or the same as with two components?
• c) Now suppose that the system consists of n components (where n is a positive integer) connected in series.  Determine the probability that this system functions successfully, as a function of n. 
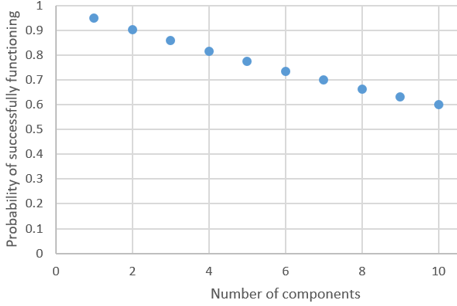
• d) Produce a graph of this function from c), for integer values of n from 1 to 10.  (Label both axes clearly.)  Also describe the behavior of this function.

If we let Si represent the event that component i functions successfully, the probability in part (a) is: Pr(S1 and S2) =  Pr(S1) × Pr(S2) = (0.95)^2 = 0.9025, using the multiplication rule for independent events.  Similarly, Pr(S1 and S2 and S3) = (0.95)^3 ≈ 0.857, which is a smaller probability.  The general expression is: Pr(S1 and S2 and … and Sn) = (0.95)^n.  This function decreases gradually, as shown in the graph below.  This decrease makes sense because, as a single bad component is all that’s needed to cause the system to fail, each additional component provides another opportunity for such failure.

Now consider a system of components that requires at least one component to function successfully in order for the system to function successfully.  (Such a system is said to be connected in parallel.)  Continue to suppose that the components operate independently, but now suppose that the probability that a single component functions successfully is 0.25. 

• e) Determine the probability that a system with two components connected in parallel functions successfully.  Also indicate the probability rule(s) that you use for this calculation.
• f) Now suppose that the system consists of three components connected in parallel.  Determine the probability that this system functions successfully.  Is this probability larger, smaller, or the same as with two components?
• g) Now suppose that the system consists of n components (where n is a positive integer) connected in parallel.  Determine the probability that this system functions successfully, as a function of n. 
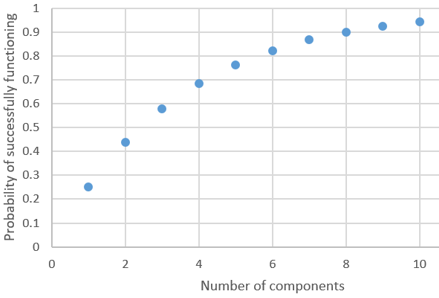
• h) Produce a graph of this function from g), for integer values of n from 1 to 10.  (Label both axes clearly.)  Also describe the behavior of this function.

The probability calculations here are: Pr(S1 or S2) = Pr(S1) + Pr(S2) – Pr(S1 and S2) = 0.25 + 0.25 – (0.25)^2 = 0.4375 by the addition rule and the multiplication rule for independent events.  An alternative solution that uses the complement rule is: Pr(S1 or S2) = 1 – Pr[(not S1) and (not S2)] = 1 – (0.75)^2 = 0.4375.  With three components, this becomes: Pr(S1 or S2 or S3) = 1 – Pr[(not S1) and (not S2) and (not S3)] = 1 – (0.75)^3 ≈ 0.578.  This probability is larger than with three components.  The general expression is: Pr(S1 or S2 or … or Sn) = 1 – Pr[(not S1) and (not S2) and … and (not Sn)] = 1 – (0.75)^n.  This function increases somewhat rapidly, as shown in the graph below.  This makes sense because, as only one successful component is needed, each additional component now provides another opportunity for the system to succeed.

Now suppose that a system consists of three components.  Two of the components are connected in parallel to form a sub-system.  That sub-system is then connected in series with the third component.  Continue to suppose that the components operate independently.  Now suppose that the probability is 0.9 that a single component functions successfully.

• i) Determine the probability that the system functions successfully.  Also indicate the probability rule(s) that you use for this calculation.

The system will function successfully if at least one of two components connected in parallel function successfully, and the third component functions successfully.  This probability can be calculated as: Pr[(S1 or S2) and S3] = Pr(S1 or S2) × Pr(S3) using the multiplication rule for independent events, which =  [Pr(S1) + Pr(S2) – Pr(S1 and S2)] × Pr(S3) using the addition rule, which = (0.9 + 0.9 – 0.81) × 0.9 = 0.99 × 0.9 = 0.891.

Finally, suppose that:

• Component A functions successfully with probability 0.8.
• Component B functions successfully with probability 0.7.
• Component C functions successfully with probability 0.6. 

You can select which two components to connect in the parallel sub-system and which component to connect in series to that sub-system. 

• j) Which component would you select to be connected in series, in order to produce the greatest probability that the system functions successfully?  Explain your answer, and also calculate the probability that the system functions successfully with your configuration.

The component connected in series is the one that has to function successfully in order for the system to function successfully.  So, the optimal arrangements puts the most reliable component (A) in that series connection and the other two in the parallel connection.  The probability is therefore: Pr[(S_B or S_C) and S_A] = Pr(S_B or S_C) × Pr(S_A) = [Pr(S_B) + Pr(S_C) – Pr(S_B and S_C)] × Pr(S_A) = [0.6 + 0.7 – (0.6)(0.7)] × 0.8 = 0.88 × 0.8 = 0.704.

This last part is my favorite question in the assignment, because it asks students to think before they calculate.  I want students to realize that the best component should be placed in the most important position.  Students can also calculate probabilities for the other two arrangements to confirm that their intuition is correct.  These probabilities turn out to be [0.6 + 0.8 – (0.6)(0.8)] × 0.7 = 0.92 × 0.7 = 0.644 and [0.7 + 0.8 – (0.7)(0.8)] × 0.6 = 0.94 × 0.6 = 0.564, both of which are indeed smaller than 0.704.

---

This concludes a three-part series on studying independent events*.  The first two posts presented examples and activities that I often use in class, and this one has suggested some out-of-class assessment questions.

* I am kicking myself about timing, because I wish that I had planned for this Independence Day series to conclude on the Fourth of July rather than on Memorial Day.

P.S. Speaking of timing, you may have noticed that this is the 100^th consecutive weekly post in the Ask Good Questions blog.  That’s such a momentous number in our base 10 system that I am going to take the next month or two off.  Thanks very much to all who have invested some of your most precious commodity – your time – into reading my blog posts.  I look forward to resuming again after this pause, and I hope very much that you will rejoin me then.

P.P.S. I also hope to see you at the U.S. Conference on Teaching Statistics (USCOTS), which will occur virtually on June 28 – July 1, with pre-conference workshops beginning on June 24.  We have lined up a terrific program to address the theme of “Expanding Opportunities.”  You can peruse the program here, register (for just $25, which can be waived) here, and read my previous blog posts about USCOTS here and here.