#99 Independence day, part 2
In post #95 (here), I described several examples for introducing students to the concept of independent events. This post presents two more examples that I like to use on Independence Day. As always, questions that I pose to students appear in italics.
I present my students with the following scenario, which is a simplified version of the famous problem discussed by Pascal and Fermat that led to the development of probability theory, described in the book The Unfinished Game, by mathematician Keith Devlin:
Suppose that Heather and Tom play a game that involves a series of coin flips. They agree that if 5 heads occur before 5 tails, then Heather wins the game. But if 5 tails occur before 5 heads, then Tom wins the game. They each agree to pay $5 to play the game, so the winner will make a profit of $5. The first five coin flips result in: H1, T2, T3, H4, H5. Unfortunately, the game is interrupted at that point and can never be finished.
a) Suggest a reasonable way to divide up the $10. The two most common responses that my students offer are: 1) give each person their $5 back, or 2) give Heather $6 and Tom $4 because Heather has won 60% of the first 5 coin flips. I tell students that these are perfectly reasonable suggestions, but mathematicians proposed to divide the $10 based on the probabilities that each player would have gone on to win the game if it had been continued.
b) Make a guess for the probability that Heather would have won the game if it had been continued. I do not ask students to reveal their guesses, but I want them to give this some thought before proceeding to analysis.
c) List the sample space of ten possible outcomes for how the game could have ended up. Use similar notation to above. This can be tricky for students, so I sometimes give a hint: Six outcomes lead to Heather’s winning, and four outcomes lead to Tom’s winning. For students who still need some help, I ask: What’s the quickest way for the game to end? At this point a student will say that Heather will win if the next two flips produce heads. Then we’re off and running. The sample space is shown below, with outcomes for which Heather wins in green and outcomes for which Tom wins in red:

d) Is it reasonable to regard these 10 outcomes as equally likely? Explain why or why not. This can give students pause, until they realize that some outcomes involve two coin flips, some three, and some four. Because of these differing numbers of flips, it’s not reasonable to regard these outcomes as equally likely.
e) Is it reasonable to regard the coin flips as independent? Explain. Assuming independence is reasonable here, because the result of any one coin flip should not affect the 50-50 chance for any other coin flips’ results.
f) For each player, determine the probability that they would win the game, if it were completed from the point of interruption. Also interpret this probability. Calculating these probabilities involves realizing that:
- An outcome of either H or T has probability 0.5 for any one flip.
- Independence of coin flips means that these 0.5 probabilities are multiplied to determine the probability for an outcome of multiple flips.
- This produces a probability of (0.5)n for all possible outcomes of n coin flips.
So, all two-flip outcomes have probability (0.5)2 = 0.25. All three-flip outcomes have probability (0.5)3 = 0.125. And all four-flip outcomes have probability (0.5)4 = 0.0625.
More formally, we can calculate the probabilities for the six outcomes in which Heather wins the game as follows:

For students who get stuck at this stage, I ask: What do we do with these six probabilities to calculate the (overall) probability that Heather would win if the game were completed from the point of interruption? Someone invariably answers that we add them, to which I respond: Yes, but why is that appropriate? This question is slightly harder, but eventually someone will point out that these six events are mutually exclusive. This sum turns out to be 0.6875.
Now I ask: What’s the easy way to calculate the probability that Tom would win the game? A student will point out that we can simply subtract Heather’s probability from one. I agree but suggest that we go ahead and figure out Tom’s probability from scratch. Then we can make sure that the two probabilities sum to one, as a way to check our work. Here are the calculations for outcomes in which Tom wins the game:
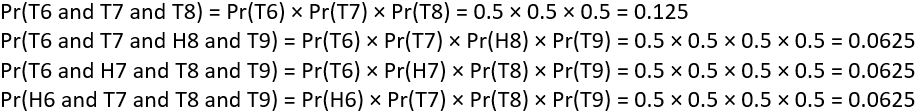
Adding these probabilities does indeed give 0.3125 for Tom’s probability of winning.
g) Based on this probability, how should the $10 be divided? If we agree to distribute the $10 proportionally to the probabilities of winning the game if it had been finished from the point of interruption, then Heather should take $6.875 and Tom $3.125. Good luck with that extra half-cent.
h) What is the probability that the game would require four more coin flips to finish? I ask this question to reinforce the idea that we can add the probabilities for the (mutually exclusive) outcomes that comprise this event. Six outcomes require four more flips, and each of those outcomes has probability (0.5)4 = 0.0625, so this probability is 6(0.0625) = 0.375.
The last example that I present on Independence Day is my favorite:
Consider four six-sided dice, all equally likely to land on any one of the six sides, but without the usual numbers 1-6 on the sides. Instead the six sides have the following numbers:
- Die A: 4, 4, 4, 4, 0, 0
- Die B: 3, 3, 3, 3, 3, 3
- Die C: 6, 6, 2, 2, 2, 2
- Die D: 5, 5, 5, 1, 1, 1
Suppose that you and I play a game in which we each select a die and roll it independently of the other. The rule is very simple: Whoever rolls the larger number wins. Being a considerate person, I let you select your die first. For whichever pair of dice that you and I might select, determine the probability that I win the game.
I wait for a student to select a die. Let’s say that she selects die B. Think about which die I should select to play against die B. I announce that I will select die A. Notice that I will roll a larger number, and therefore win the game, whenever die A lands on 4. Because four of the six sides of die A have the number 4, the probability that I win is 4/6 = 2/3 ≈ 0.6667.
Now I ask my students to make a different initial selection. Let’s say that someone selects die C. Think about which die I should select to play against die C. This time I will select die B. Notice that I will roll a larger number, and therefore win the game, whenever die C lands on 2. Because four of the six sides of die C have the number 2, the probability that I win is again 4/6 = 2/3 ≈ 0.6667.
At this point, some students begin to catch on, but I persist and ask for a different initial selection. Now suppose that a student selects die D. Think about which die I should select to play against die D. Now I will select die C. Why is the probability calculation more complicated this time? Because we have to two ways for me to win, one of which depends on what number you roll. In other words, we need to consider intersections of events. This time I will win when die C lands on 6, or when die C lands on 2 and die D lands on 1. We could express this as: Pr[C6 or (C2 and D1)]. We can calculate this as: Pr(C6) + Pr(C2)×Pr(D1), where the multiplication is justified because C2 and D1 are independent events. This works out to be (surprise, surprise): (2/6) + (4/6)×(3/6) = 2/3 ≈ 0.6667.
Most students have caught on by now, but I insist on finishing this story. The only other option is for you to select die A, in which case I will select die D. Can you guess the probability that I win this time? No surprise, this probability is now: Pr[D5 or (D1 and A0)] = (3/6) + (3/6)×(2/6) ≈ 0.6667.
What’s the best way to play this game? Convince your opponent to select a die first. No matter which die they choose, you can always select a die that gives you a 2/3 chance of winning the game.
What mathematical property does this example violate? Usually, one student will tentatively suggest the correct answer, that this example violates the transitive property. This property would say that because die A beats die B 2/3 of the time, and die B beats die C 2/3 of the time, and die C beats die D 2/3 of the time, you would expect die A to beat die D at least 2/3 of the time. But the opposite is true, because we have established that die A beats die D only 1/3 of the time. This is sometimes called an example of non-transitive dice.
I find this example amusing, and I think some of my students agree. I enjoy ending our Independence Day class with this flourish.
These two examples do not introduce students to new probability concepts or methods or rules. They simply provide opportunities to apply the multiplication rule for independent events. The unfinished game example gives me a chance to mention the history of probability. The non-transitive dice example is just plain fun.
I also want to describe some quiz and homework questions that I ask as a follow-up to these Independence Day examples, but I’ll save those for part 3 of this series.

Thhis was great to read
LikeLike