Ask Good Questions

#45 Simulation-based inference, part 3

I’m a big believer in introducing students to concepts of statistical inference through simulation-based inference (SBI).  I described activities for introducing students to the concepts of p-value and strength of evidence in posts #12 (here) and #27 (here).  The examples in both of these previous posts concerned categorical variables.  Now I will describe an activity for leading students to use SBI to compare two groups with a numerical response.  As always, questions that I pose to students appear in italics.

---

Here’s the context for the activity: Researchers randomly assigned 14 male volunteers with high blood pressure to one of two diet supplements – fish oil or regular oil.  The subjects’ diastolic blood pressure was measured at the beginning of the study and again after two weeks.  Prior to conducting the study, researchers conjectured that those with the fish oil supplement would tend to experience greater reductions in blood pressure than those with the regular oil supplement*.

* I read about this study in the (wonderfully-titled) textbook The Statistical Sleuth (here).  The original journal article can be found here.

a) Identify the explanatory and response variables.  Also classify each as categorical or numerical.

I routinely ask this question of my students at the start of each activity (see post #11, Repeat after me, here).  The explanatory variable is type of diet supplement, which is categorical and binary.  The response variable is reduction in diastolic blood pressure, which is numerical.

b) Is this a randomized experiment or an observational study?  Explain.

My students know to expect this question also.  This is a randomized experiment, because researchers assigned each participant to a particular diet supplement.

c) State the hypotheses to be tested, both in words and in symbols.

I frequently remind my students that the null hypothesis is typically a statement of no difference or no effect.  In this case, the null hypothesis stipulates that there’s no difference in blood pressure reductions, on average, between those who could be given a fish oil supplement as compared a regular oil supplement.  The null hypothesis can also be expressed as specifying that the type of diet supplement has no effect on blood pressure reduction.  Because of the researchers’ prior conjecture, the alternative hypothesis is one-sided: Those with a fish oil supplement experience greater reduction in blood pressure, on average, than those with a regular oil supplement. 

In symbols, these hypotheses can be expressed as H₀: mu_fish = mu_reg vs. H_a: mu_fish > mu_reg.  Some students use x-bar symbols rather than mu in the hypotheses, which gives me an opportunity to remind them that hypotheses concern population parameters, not sample statistics.

I try to impress upon students that hypotheses can and should be determined before the study is conducted, prior to seeing the data.  I like to reinforce this point by asking them to state the hypotheses before I show them the data.

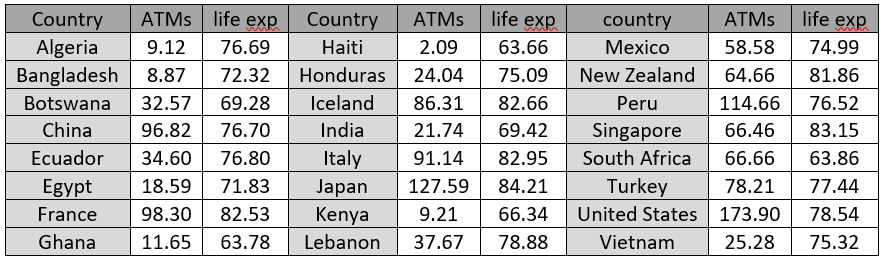
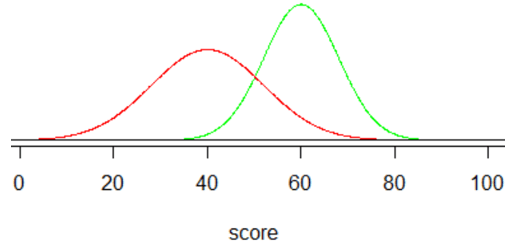
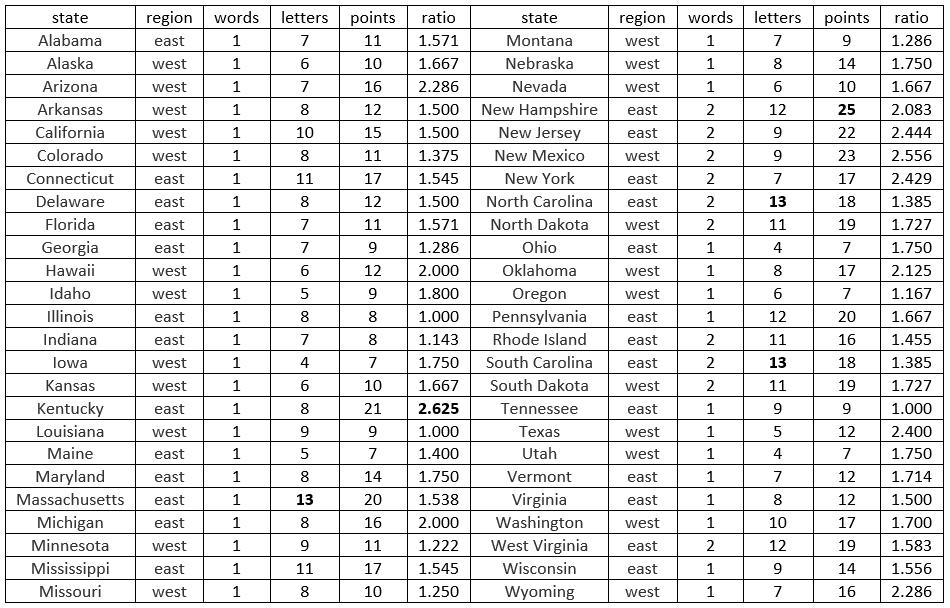
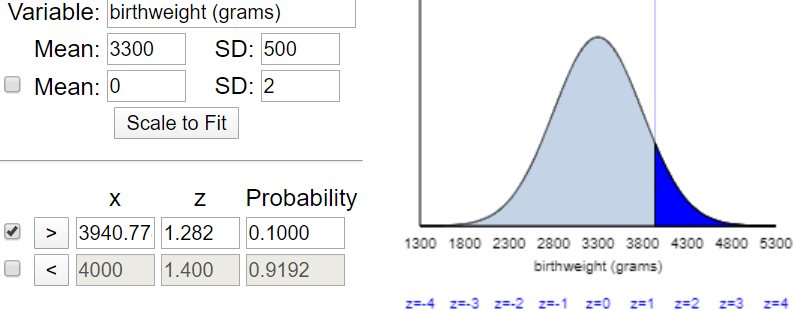
Here are dotplots showing the sample data on reductions in systolic blood pressure (measured in millimeters of mercury) for these two groups (all data values are integers):

d) Calculate the average blood pressure reduction in each group. What symbols do we use for these averages?  Also calculate the difference in these group means (fish oil group minus regular oil group).  Are the sample data consistent with the researchers’ conjecture?  Explain.

The group means turn out to be: x-bar_fish = 46/7 ≈ 6.571 mm for the fish oil group, x-bar_reg = -8/7 ≈ -1.143 for the regular oil group.  This difference is 54/7 ≈ 7.714 mm.  The data are consistent with the researchers’ conjecture, because the average reduction was greater with fish oil than with regular oil.

e) Is it possible that there’s really no effect of the fish oil diet supplement, and random chance alone produced the observed differences in means between these two groups?

I remind students that they’ve seen this question, or at least its very close cousin, before.  We asked this same question about the results of the blindsight study, in which the patient identified the non-burning house in 14 of 17 trials (see post #12, here).  We also asked this about the results of the penguin study, in which penguins with a metal band were 30 percentage points more likely to die than penguins without a metal band (see post #27, here).  My students know that the answer I’m looking for has four letters: Sure, it’s possible.

But my students also know that the much more important question is: How likely is it?  At this point in class I upbraid myself for using the vague word and ask: What does it mean here?  I’m very happy when a student explains that I mean to ask how likely it is to obtain sample mean reductions at least 7.714 mm apart, favoring fish oil, if type of diet supplement actually has no effect on blood pressure reduction.

f) How can we investigate how surprising it would be to obtain results as extreme as this study’s, if in fact there were no difference between the effects of fish oil and regular oil supplements on blood pressure reduction?

Students have seen different versions of this question before also.  The one-word answer I’m hoping for is: Simulate!

g) Describe (in detail) how to conduct the simulation analysis to investigate the question in part f).

Most students have caught on to the principle of simulation at this point, but providing a detailed description in this new scenario, with a numerical response variable, can be challenging.  I follow up with: Can we simply toss a coin as we did with the blindsight study?  Clearly not.  We do not have a single yes/no variable.  Can we shuffle and deal out cards with two colors?  Again, no.  The two colors represented success and failure, but we now have numerical responses.  How can we use cards to conduct this simulation?  Some students have figured out that we can write the numerical responses from the study onto cards.  What does each card represent?  One of the participants in the study.  How many cards do we need?  Fourteen, one for each participant.  What do we do with the cards?  Shuffle them.  And then what?  Separate them into two groups of 7 cards each.  What does this represent?  Random assignment of the 14 subjects into one of the two diet supplement groups.  Then what?  Calculate the average of the response values in each group.  And then?  Calculate the difference in those two averages, being careful to subtract in the same order that we did before: fish oil group minus regular oil group.  Great, what next?  This one often stumps students, until they remember that we need to repeat this process, over and over again, until we’ve completed a large number of repetitions.

Before we actually conduct this simulation, I ask:

h) Which hypothesis are we assuming to be true as we conduct this simulation?  This gives students pause, until they remember that we always assume the null hypothesis to be true when we conduct a significance test.  They can also state this in the context of the current study: that there’s no difference, on average, between the blood pressure reductions that would be achieved with a fish oil supplement versus a regular oil supplement.  I also want them to think about how it applies in this case: How does this assumption manifest itself in our simulation process?  This is a hard question.  I try to tease out the idea that we’re assuming the 14 participants were going to experience whatever blood pressure reduction they did no matter which group they had been assigned to.

---

Now, finally, having answered all of these preliminary questions, we’re ready to do something.  Sometimes I provide index cards to students and ask them to conduct a repetition or two of this simulation analysis by hand.  But I often skip this part* and proceed directly to conduct the simulation with a computer. 

* I never skip the by-hand simulation with coins in the blindsight study or with playing cards in the penguin study, because I think the tactile aspect helps students to understand what the computer does.  But the by-hand simulation takes considerably more time in this situation, with students first writing the 14 response values on 14 index cards and later having to calculate two averages.  My students have already conducted tactile simulations with the previous examples, so I trust that they can understand what the computer does here.

I especially like that this applet (here), designed by Beth Chance, illustrates the process of pooling the 14 response values and then re-randomly assigning them between the two groups.  The first steps in using the applet are to clear the default dataset and enter (or paste) the data for this study.  (Be sure to click on “Use Data” after entering the data.)  The left side of the screen displays the distributions and summary statistics.  Then clicking on “Show Shuffle Options” initiates simulation capabilities on the right side of the screen.  I advise students to begin with the “Plot” view rather than the “Data” view.

i) Click on “Shuffle Responses” to conduct one repetition of the simulation.  Describe what happens to the 14 response values in the dotplots.  Also report the resulting value of the difference in group means (again taking the fish oil group minus the regular oil group).

This question tries to focus students’ attention on the fact that the applet is doing precisely what we described for the simulation process: pooling all 14 (unchanging) response values together and then re-randomizing them into two groups of 7.

j) Continue to click on “Shuffle responses” for a total of 10 repetitions.  Did we obtain the same result (for the difference in group means) every time?  Are any of the difference in groups means as large as the value observed in the actual study: 7.714 mm?

Perhaps it’s obvious that the re-randomizing does not produce the same result every time, but I think this is worth emphasizing.  I also like to keep students’ attention on the key question of how often the simulation produces a result as extreme as the actual study.

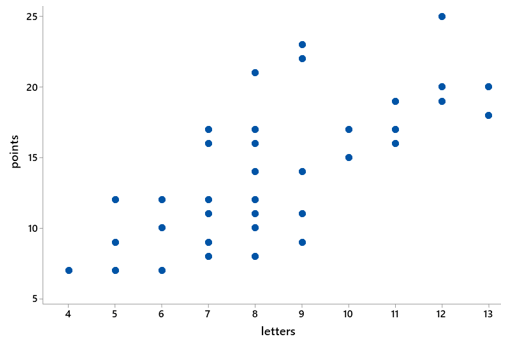
k) Now enter 990 for the number of shuffles, which will produce a total of 1000 repetitions.  Consider the resulting distribution of the 1000 simulated differences in group means.  Is the center where you would expect?  Does the shape have a recognizable pattern?  Explain.

Here is some output from this simulation analysis:

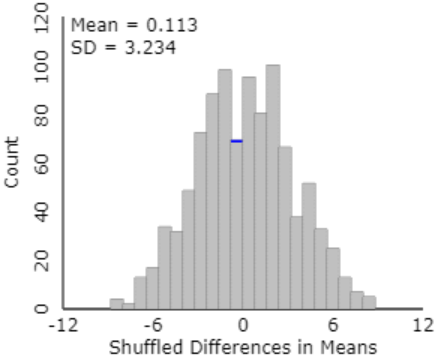
The mean is very close to zero.  Why does this make sense?  The assumption behind the simulation is that type of diet supplement has no effect on blood pressure reduction, so we expect the difference in group means (always subtracting in the same order: fish oil group minus regular oil group) to include about half positive values and half negative values, centered around zero.  The shape of this distribution is very recognizable at this point of the course: approximately normal.

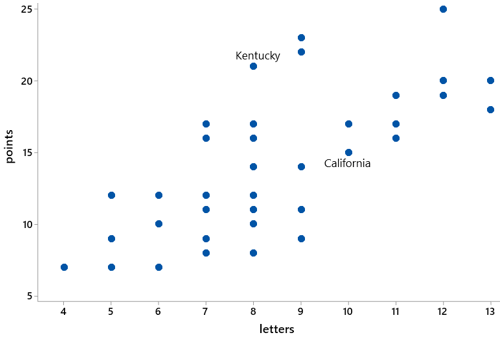
l) Use the Count Samples feature of the applet to determine the approximate p-value, based on the simulation results.  Also describe how you determine this.

The applet does not have a “Calculate Approximate P-value” button.  That would have been easy to include, of course, but the goal is for students to think through how to determine this for themselves.  Students must realize that the approximate p-value is the proportion of the 1000 simulated differences in group means that are 7.714 or larger.  They need to enter the value 7.714 in the box* next to “Count Samples Greater Than” and then click on “Count.”  The following output shows an approximate p-value of 0.006:

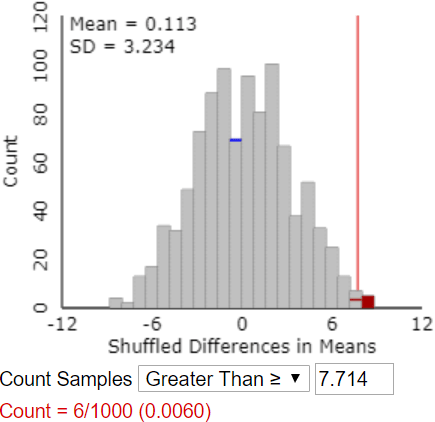
* If a student enters a different value here, the applet provides a warning that this might not be the correct value, but it proceeds to do the count.

m) Interpret what this (approximate) p-value means.

This is usually a very challenging question.  But based on simulation-based inference, students need not memorize this interpretation of a p-value.  Instead, they simply have to describe what’s going on in the graph of simulation results: If there were no effect of diet supplement on blood pressure reductions, then about 0.6% of random assignments would produce a difference in sample means, favoring the fish oil group, of 7.714 or greater.  I also like to model conveying this idea with a different sentence structure, such as: About 0.6% of random assignments would produce a difference in sample means, favoring the fish oil group, of 7.714 or greater, assuming that there were no effect of diet supplement on blood pressure reductions.  The hardest part of this for most students is remembering to include the if or assuming part of this sentence.

---

Now we are ready to draw some conclusions.

n) Based on this simulation analysis, do the researchers’ data provide strong evidence that the fish oil supplement produces a greater reduction in blood pressure, on average, than the regular oil supplement?  Also explain the reasoning process by which your conclusion follows from the simulation analysis.

The short answer is yes, the data do provide strong evidence that the fish oil supplement is more helpful for reducing blood pressure than the regular oil supplement.  I hope students answer yes because they understand the reasoning process, not because they’ve memorized that a small p-value means strong evidence of …  I do not consider “because the p-value is small” to be an adequate explanation of the reasoning process.  I’m looking for something such as: “It would be very unlikely to obtain a difference in group mean blood pressure reductions of 7.714mm or greater, if fish oil were no better than regular oil.  But this experiment did find a difference in group means of 7.714mm.  Therefore, we have strong evidence against the hypothesis of no effect, in favor of concluding that fish oil does have a beneficial effect on blood pressure reduction.”

At this point I make a show of pointing out that I just used the important word effect, so I then ask:

o) Is it legitimate to draw a cause-and-effect conclusion between the fish oil diet and greater blood pressure reductions?  Justify your answer.

Yes, a cause-and-effect conclusion is warranted here, because this was a randomized experiment and the observed difference in group means is unlikely to occur by random assignment alone if there were no effect of diet supplement type on blood pressure reduction.

Now that I’ve asked about causation, I follow up with a final question about generalizability:

p) To what population is it reasonable to generalize the results of this study?

Because the study included only men, it seems unwise to conclude that women would necessarily respond to a fish oil diet supplement in the same way.  Also, the men in this study were all volunteers who suffered from high blood pressure.  It’s probably best to generalize only to men with high blood pressure who are similar to those in this study. 

---

Whew, that was a lot of questions*!  I pause here to give students a chance to ask questions and reflect on this process.  I also reinforce the idea, over and over, that this is the same reasoning process they’ve seen before, with the blindsight study for a single proportion and with the penguin study for comparing proportions.  The only difference now is that we have a numerical response, so we’re looking at the difference in means rather than proportions.  But the reasoning process is the same as always, and the interpretation of p-value is the same as always, and the way we assess strength of evidence is the same as always.

* We didn’t make it to part (z) this time, but this post is not finished yet …

Now I want to suggest three extensions that you could consider, either in class or on assignments, depending on your student audience, course goals, and time constraints.  You could pursue any or all of these, in any order.

Extension 1: Two-sample t-test

q) Conduct a two-sample t-test of the relevant hypotheses.  Report the value of the test statistic and p-value.  Also summarize your conclusion.

The two-sample (unpooled) test statistic turns out to be t = 3.06, with a (one-sided) p-value of ≈ 0.007*.  Based on this small p-value, we conclude that the sample data provide strong evidence that fish oil reduced blood pressure more, on average, than regular oil.

* Whenever this fortunate occurrence happens, I tell students that this is a p-value of which James Bond would be proud!

r) How does the result of the t-test compare to that of the simulation analysis?

The result are very similar.  The approximate p-value from the simulation analysis above was 0.006, and the t-test gave an approximate p-value of 0.007. 

Considering how similar these results are, you might be wondering why I recommend bothering with the simulation analysis at all.  The most compelling reason is that the simulation analysis shows students what a p-value is: the probability of obtaining such a large (or even larger) difference in group means, favoring the fish oil group, if there were really no difference between the treatments.  I think this difficult idea comes across clearly in the graph of simulated results that we discussed above.  I don’t think calculating a p-value from a t-distribution helps to illuminate this concept.

---

Extension 2: Comparing medians

Another advantage of simulation-based inference is that it provides considerable flexibility with regard to the choice of statistic to analyze.  For example, could we compare the medians of the two groups instead of their means?  From the simulation-based perspective: Sure!  Do we need to change the analysis considerably?  Not at all!  Using the applet, we simply select the difference in medians rather than the difference in means from the pull-down list of statistic options on the left side.  If we were writing our own code, we would simply replace mean with median. 

s) Before we conduct a simulation analysis of the difference in median blood pressure reductions between the two groups, first predict what the distribution of 1000 simulated differences in medians will look like, including the center and shape of the distribution. 

One of these is much easier to anticipate than the other: We can expect that the center will again be near zero, again because the simulation operates under the assumption of no difference between the treatments.  But medians often do not follow a predictable, bell-shaped curve like means often do, especially with such small sample sizes of 7 per group.

t) Use the applet to conduct a simulation analysis with 1000 repetitions, examining the difference in medians between the groups.  Describe the resulting distribution of the 1000 simulated differences in medians.

Here is some output:

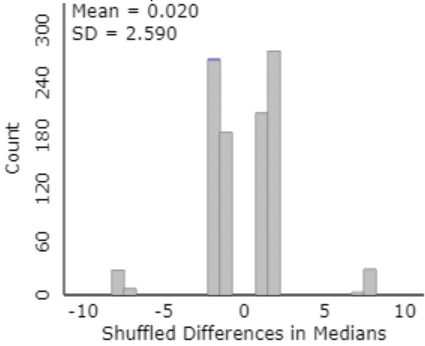
The center is indeed close to zero.  The shape of this distribution is fairly symmetric but very irregular.  This oddness is due to the very small sample sizes and the many duplicate data values.  In fact, there are only eight possible values for the difference in medians: ±8, ±7, ±2, and ±1. 

u) How do we determine the approximate p-value from this simulation analysis?  Go ahead and calculate this.

This question makes students stop and think.  I really want them to be able to answer this correctly, because they’re not really understanding simulation-based inference if they can’t.  I offer a hint: Do we plug in 7.714 again and count beyond that value?  Most students realize that the answer is no, because 7.714 was the difference in group means, not medians, in the actual study.  Then where do we count?  Many students see that we need to count how often the simulation gave a result as extreme as the difference in medians in the actual study, which was 8mm.

Here’s the same graph, with results for which the difference in sample medians is 8 or greater colored in red:

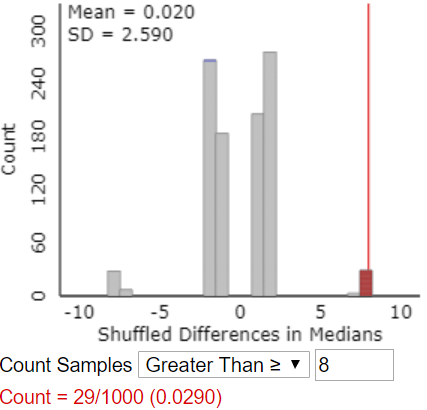
v) Compare the results of analyzing medians rather than means.

We obtained a much smaller p-value when comparing means (0.006) than when comparing medians (0.029).  In both cases, we have reasonably strong evidence that fish oil is better than regular oil for reducing blood pressure, but we have stronger evidence based on means than on medians.

---

Extension 3: Exact randomization test

What we’ve simulated above is often called a randomization test.  Could we determine the p-value for the randomization test exactly rather than approximately with simulation?  Yes, in principle, but this would involve examining all possible ways to randomly assign subjects between the treatment groups.  In most studies, there are often too many combinations to analyze efficiently.  In this study, however, the number of participants is small enough that we can determine the exact randomization distribution of the statistic.  I only ask the following questions in courses for mathematically inclined students.

w) In many ways can 14 people be assigned to two groups of 7 people each?

This is what the combination (also called a binomial coefficient) 14-choose-7 tells us.  This is calculated as: 14! / (7! ×7!) = 3432.  That’s certainly too many to list out by hand, but that’s a pretty small number to tackle with some code.

x) Describe what to do, in principle, to determine the exact randomization distribution.

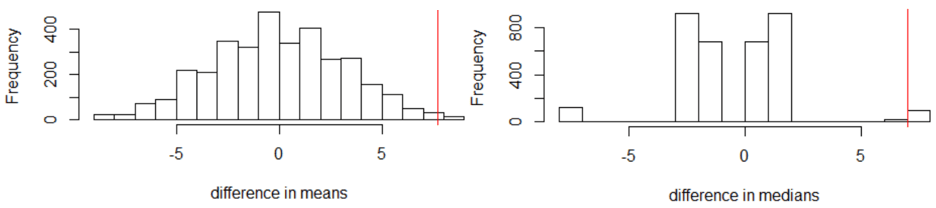
We continue to assume that the 14 participants were going to obtain the same blood pressure reduction values that they did, regardless of which diet supplement group they had been assigned to.  For each of these 3432 ways to split the 14 participants into two groups of 7 each, we calculate the mean/median of data values in each group, and then we calculate the difference in means/medians (fish oil group minus regular oil group).  I’ll spare you the coding details.  Here’s what we get, with difference in means on the left, difference in medians on the right:

y) How would you calculate the exact p-values?

For the difference in means, we need to count how many of the 3432 possible random assignments produce a difference in means of 7.714 or greater.  It turns out that only 31 give such an extreme difference, so the exact p-value is 31/3432 ≈ 0.009.

If we instead compare medians, it turns out that exactly 100 of the 3432 random assignments produce a difference in medians of 8 or greater, for a p-value of 100/3432 ≈ 0.029.  Interestingly, 8 is the largest possible difference in medians, but there are 100 different ways to achieve this value from the 14 data values.

z) Did the simulation results come close to the exact p-values?

Yes.  The approximate p-value based on comparing means was 0.006, very close to the exact p-value of 0.009.  Similarly, the approximate p-value based on comparing medians was 0.029, the same (to three decimal places) as the exact p-value.

---

If you’re intrigued by simulation-based inference but reluctant to redesign your entire course around this idea, I recommend sprinkling a bit of SBI into your course.  Depending on how many class sessions you can devote to this, I recommend these sprinkles in this order:

1. Inference for a single proportion with a 50/50 null, as with the blindsight study of post #12 (here)
2. Comparing two proportions, as with the penguin study of post #27 (here)
3. Comparing two means or medians, as with the fish oil study in this post
4. Inference for correlation, as with the draft lottery toward the end of post #9 (here)

For each of these scenarios, I strongly suggest that you introduce the simulation-based approach before the conventional method.  This can help students to understand the logic of statistical inference before getting into the details.  I also recommend emphasizing that the reasoning process is the same throughout these scenarios.  After leading students through the simulation-based approach, you can impress upon students that the conventional methods are merely shortcuts that predict what the simulation results would look like without bothering to conduct the simulation.

---

P.S. Here is a link to the datafile for this activity:

P.P.S. I provided a list of textbooks that prominently include simulation-based inference at the end of post #12 (here).

P.P.P.S. I dedicate this post to George Cobb, who passed away in the last week.  George had a tremendous impact on my life and career through his insightful and thought-provoking writings and also his kind mentoring and friendship. 

George’s after-dinner address at the inaugural U.S. Conference on Teaching Statistics in 2005 inspired many to pursue simulation-based inference for teaching introductory statistics.  His highly influential article based on this talk, titled “The Introductory Statistics Course: A Ptolemaic Curriculum?,” appeared in the inaugural issue of Technology Innovations in Statistics Education (here).  George wrote: “Before computers statisticians had no choice. These days we have no excuse. Randomization-based inference makes a direct connection between data production and the logic of inference that deserves to be at the core of every introductory course.”

George’s writings contributed greatly as my Ask Good Questions teaching philosophy emerged.  At the beginning of my career, I read his masterful article “Introductory Textbooks: A Framework for Evaluation,” in which he simultaneously reviewed 16 textbooks for the Journal of the American Statistical Association (here).  Throughout this review George repeated the following mantra over and over: Judge a textbook by its exercises, and you cannot go far wrong.  This sentence influenced me not only for its substance – what teachers ask students to do is more important than what teachers tell students – but also for its style – repeating a pithy phrase can leave a lasting impression. 

Another of my favorite sentences from George, which has stayed in my mind and influenced my teaching for decades, is: Shorn of all subtlety and led naked out of the protective fold of education research literature, there comes a sheepish little fact: lectures don’t work nearly as well as many of us would like to think (here).

I had the privilege of interviewing George a few years ago for the Journal of Statistics Education (here).  His wisdom, humility, insights, and humor shine throughout his responses to my questions.

#39 Batch testing

One of my favorite examples for studying discrete random variables and expected values involves batch testing for a disease.  I would not call this a classic probability problem, but it’s a fairly common problem that appears in many probability courses and textbooks.  I did not intend to write a blog post about this, but I recently read (here) that the Nebraska Public Health Lab has implemented this idea for coronavirus testing.  I hope this topic is timely and relevant, as so many teachers meet with their students remotely in these extraordinary circumstances.  As always, questions that I pose to students appear in italics.

---

Here are the background and assumptions: The idea of batch testing is that specimens from a group of people are pooled together into one batch, which then undergoes one test.  If none of the people has the disease, then the batch test result will be negative, and no further tests are required.  But if at least one person has the disease, then the batch test result will be positive, and then each person must be tested individually.  Let the random variable X represent the total number of tests that are conducted.  Let’s start with a disease probability of p = 0.1 and a sample size of n = 8.  Assume that whether or not a person has the disease is independent from person to person.

a) What are the possible values of X?  When students need a hint, I say that there are only two possible values.  If they need more of a hint, I ask about what happens if nobody in the sample has the disease, and what happens if at least one person in the sample has the disease.  If nobody has the disease, then the process ends after that 1 test. But if at least one person has the disease, then all 8 people need to undergo individual tests.  The possible values of X are therefore 1 and 9.

b) Determine the probability that only one test is needed.  For students who do not know where to start, I ask: What must be true in order that only one test is needed?  They should recognize that only one test is needed when nobody has the disease.  Because we’re assuming independence, we calculate the probability that nobody has the disease by multiplying each person’s probability of not having the disease.  Each person has probability 0.9 of not having the disease, so the probability that nobody has the disease is (0.9)^8 ≈ 0.430.

c) Determine the probability for the other possible value of X.  Because there are only two possible values, we can simply subtract the other probability from 1, giving 1 – (0.9)^8 ≈ 0.570.  I point out to students that this is the probability that at least one person in the sample has the disease. I also note that it’s often simplest to calculate such a probability with the complement rule: Pr(at least one) = 1 – Pr(none).

d) Interpret these probabilities with sentences that begin “There’s about a _____ % chance that __________ .”  I like to give students practice with expressing probabilities in sentence form: There’s about a 43% chance that only one test is needed, and about a 57% chance that nine tests are needed.

e) Display the probability distribution of X in a table.  For a discrete random variable, a probability distribution consists of its possible values and their probabilities.  We can display this probability distribution as follows:

f) Determine the expected value of the number of tests that will be conducted.  With only two possible values, this is a very straightforward calculation: E(X) = 1×[(.9)^8] + 9×[1–(.9)^8] = 9 – 8×[(.9)^8] ≈ 5.556 tests.

g) Interpret what this expected value means.  In post #18 (What do you expect, here), I argued that we should adopt the term long-run average in place of expected value.  The interpretation is that if we were to repeat this batch testing process for a large number of repetitions, the long-run average number of tests that we would need would be very close to 5.556 tests.

h) Which is more likely – that the batch procedure will require one test or nine tests?  This is meant to be an easy one: It’s more likely, by a 57% to 43% margin, that the procedure will require nine tests.

i) In what sense is batch testing better than simply testing each individual at the outset?  This is the key question, isn’t it?  Part (h) suggests that perhaps batch testing is not helpful, because in any one situation you’re more likely to need more tests with batch testing than you would with individual testing from the outset.  But I point students who need a hint back to part (g): In the long run, you’ll only need an average of 5.562 tests with batch testing, which is fewer than the 8 tests you would always need with individual testing.  If you need to test a large number of people, and if tests are expensive or in limited supply, then batch testing provides some savings on the number of tests needed.

---

The questions above used particular values for the number of people (n) and the probability that an individual has the disease (p).  Next I ask students to repeat their analysis for the general case.

j) Specify the probability distribution of X, in terms of n and p.  If students need a hint, I remind them that there are still only two possible values of X.  If nobody has the disease, only 1 test is needed.  If at least one person has the disease, then (n+1) tests are needed.  The probability that only 1 test is needed is the product of each individual’s probability of not having the disease: (1–p)^n.  Then the complement rule establishes that the probability of needing (n+1) tests is: 1–(1–p)^n.  The probability distribution of X is shown in the table:

k) Determine the expected value of the number of tests, as a function of n and p.  The algebra gets a bit messy, but setting this up is straightforward: E(X) = 1×[(1–p)^n] + (n+1)×[1–(1-p)^n], which simplifies to n+1–n×[(1–p)^n].

l) Verify that this function produces the expected value that you calculated above when n = 8 and p = 0.1.  I want students to develop the habit of mind to check their work like this on their own, but I can model this practice by asking this question explicitly.  Sure enough, plugging in n = 8 and p = 0.1 produces E(X) = 5.556 tests.

m) Graph E(X) as a function of n, for values from 2 to 50, with a fixed value of p = 0.1.  Students can use whatever software they like to produce this graph, including Excel:

n) Describe the behavior of this function.  This is an increasing function.  This makes sense because having more people produces a greater chance that at least one person has the disease, so this increases the expected number of tests.  The behavior of the function is most interesting with a small sample size.  The function is slightly concave up for sample sizes less than 10, and then close to linear for larger sample sizes.

o) Determine the values of n for which batch testing is advantageous compared to individual testing, in terms of producing a smaller expected value for the number of tests.  Here’s the key question again.  We are looking in the graph for values of n (number of people) for which the expected number of tests (represented by the dots) is less than the value of n.  The gray 45-degree line in the following graph makes this comparison easier to see:

From this graph, we see that the expected number of tests with 25 people is a bit less than 25, and the expected number of tests with 35 people is slightly greater than 35, but it’s hard to tell from the graph with 30 people.  We can zoom in on some values to see where the expected number of tests begins to exceed the sample size:

This zoomed-in table reveals that the expected number of tests is smaller with batch testing, as compared to individual testing, when there are 33 or fewer people.  (Remember that we have assumed that the disease probability is p = 0.1 here.)

p) Now graph E(X) as a function of p, for values from 0.01 to 0.50 in multiples of 0.01, with a fixed value of n = 8.  Here is what Excel produces:

q) Describe the behavior of this function.  This function is also increasing, indicating that we expect to need more tests as the probability of an individual having the disease increases.  The rate of increase diminishes gradually as the probability increases, approaching a limit of 9 tests.

r) Determine the values of p for which batch testing is advantageous compared to individual testing.  Looking at the graph, we see that the expected number of tests is less than 8 for values of p less than 0.2.  We also see that the exact cutoff value is a bit larger than 0.2, but we need to perform some algebra to solve the inequality:

s) Express your finding from the previous question in a sentence.  I ask this question because I worry that students become so immersed with calculations and derivations that they lose sight of the big picture.  I hope they’ll say something like: With a sample size of 8 people, the expected number of tests with batch testing is less than for individual testing whenever the probability that an individual has the disease is less than approximately 0.2289.

---

Here’s a quiz question that I like to ask following this example, to assess whether students understood the main idea: The following table shows the expected value of the number of tests with batch testing, for several values of n and p:

a) Show how the value 47.15 was calculated.  b) Circle all values in the table for which batch testing is advantageous compared to individual testing.

Students should answer (a) by plugging n = 50 and p = 0.05 into the expected value formula that we derived earlier: 50 + 1 – 50×[(1–0.05)^50] ≈ 47.15.  To answer part (b), students should circle the values in bold below, because the expected number of tests is less than n, the number of people who need testing:

---

Here is an extension of this example that I like to use on assignments and exams: Suppose that 8 people to be tested are randomly split into two groups of 4 people each.  Within each group of 4 people, specimens are combined into a single batch to be tested.  If anyone in the batch has the disease, then the batch test will be positive, and those 4 people will need to be tested individually.  Assume that each person has probability 0.1 of having the disease, independently from person to person.  a) Determine the probability distribution of Y, the total number of tests needed.  b) Calculate and interpret E(Y).  c) Is this procedure better than batch-testing all 8 people in this case?  Justify your answer.

Some students struggle with the most basic step here, recognizing that the possible values for the total number of tests are 2, 6, and 10.  The total number of tests will be just 2 if nobody has the disease.  If one batch has nobody with the disease and the other batch has at least one person with the disease, then 4 additional tests are needed, making a total of 6 tests.  If both batches have at least one person with the disease, then 8 additional tests are needed, which produces a total of 10 tests.

The easiest probability to calculate is the best-case scenario Pr(Y = 2), because this requires that none of the 8 people have the disease: (.9)^8 ≈ 0.430.  Now students do not have the luxury of simply subtracting this from one, so they must calculate at least one of the other probabilities.  Let’s calculate the worst-case scenario Pr(Y = 10) next, which means that at least one person in each batch has the disease: (1–.9^4)×(1–.9^4) ≈ 0.118. 

At this point students can determine the remaining probability by subtracting the sum of the other two probabilities from one: Pr(Y = 6) = 1 – Pr(Y = 2) – Pr(Y = 10) ≈ 0.452.  For students who adopt the good habit of solving such problems in multiple ways as a check on their calculations, they could also calculate Pr(Y = 6) as: 2×(.9^4)×(1–.9^4).  It’s easy to forget the 2 here, which is necessary because either of the two batches could be the one with the disease. 

The following table summarizes these calculations to display the probability distribution of Y:

The expected value turns out to be: E(Y) = 2×0.430 + 6×0.452 + 8×0.118 ≈ 4.751 tests*.  If we were to repeat this testing procedure a large number of times, then the long-run average number of tests needed would be very close to 4.751.  This is smaller than the expected value of 5.556 tests when all eight specimens are batched together.  This two-batch strategy is better than the one-batch plan, and also better than simply conducting individual tests. In the long run, the average number of tests is smallest with the two-batch plan.

* An alternative method for calculating this expected value is to double the expected number of tests with 4 people from our earlier derivation: 2×[4+1–4×(.9^4)] ≈ 4.751 tests.

This is a fairly challenging exam question, so I give generous partial credit.  For example, I make part (a) worth 6 points, and students earn 3 points for correctly stating the three possible values.  They earn 1 point for any one correct probability, and they also earn a point if their probabilities sum to one.  Part (b) is worth 2 points.  Students can earn full credit on part (b) by showing how to calculate an expected value correctly, even if their part (a) is incorrect.  An exception is that I deduct a point if their expected value is beyond what I consider reasonable in this context.  Part (c) is also worth 2 points, and students can again earn full credit regardless of whether their answer to part (b) is correct, by comparing their expected value to 5.556 and making the appropriate decision.

---

As I conclude this post, let me emphasize that I am not qualified to address how practical (or impractical) batch testing might be in our current situation with coronavirus.  My point here is that students can learn that probabilistic thinking can sometimes produce effective strategies for overcoming problems.  More specifically, the batch testing example can help students to deepen their understanding of probability rules, discrete random variables, and expected values. 

This example also provides an opportunity to discuss timely and complex issues about testing for a disease when tests are scarce or expensive.  One issue is the difficulty of estimating the value of p, the probability than an individual to be tested has the disease.  In the rapidly evolving case of coronavirus, this probability varies considerably by place, time, and health status of the people to be tested.  Here are some data about estimating the probability that an individual to be tested has the disease:

• The COVID Tracking Project (here) reports that as of March 29, the United States has seen 139,061 positive results in 831,351 coronavirus tests, for a percentage of 16.7%.  The vast majority who have taken a test thus far have displayed symptoms or been in contact with others who have tested positive, so this should not be regarded as an estimate of the prevalence of the disease in the general public.  State-by-state data can be found here.
• Also as of the afternoon of March 29, the San Luis Obispo County (where I live) Public Health Department has tested 404 people and obtained 33 positive results (8.2%).  Another 38 positive test results in SLO County have been reported by private labs, but no public information has been released about the number of tests conducted by these private labs.  Information for SLO is updated daily here.
• Iceland has conducted tests much more broadly than most countries, including individuals who do not have symptoms (see here).  As of March 29, Iceland’s Directorate of Health is reporting (here) that 1020 of 15,484 people (6.6%) have tested positive for coronavirus.

Also note that the assumption of independence in the batch testing example is unreasonable if the people to be tested have been in contact with each other.  In the early days of this pandemic, one criterion for being tested has been proximity to others who have tested positive.  Another note is that the batch testing analysis does not take into account that test results may not always be correct.

Like everyone, I hope that more and more tests for coronavirus become widely available in the very near future.

P.S. For statistics teachers who are making an abrupt transition to teaching remotely, I recommend the StatTLC (Statistics Teaching and Learning Corner) blog (here), which has recently published several posts with helpful advice on this very timely topic.

#37 What’s in a name?

Delivered by Juliet on her iconic balcony, Shakespeare’s poetic what’s in a name speech is one of the most famous in the English language. 

What does this have to do with teaching introductory statistics?  Well, there’s a lot of data that one could collect on students’ names.  An obvious but boring example is to count the number of letters in a name.  A more fun, albeit silly, option is to determine the number of Scrabble points in a name.  I often collected these data from students early in my teaching career.

I have abandoned this practice in recent years, primarily because I want students to analyze more important and consequential datasets.  But I am starting to rethink this for two reasons.  First, there’s nothing wrong with occasionally using a dataset that’s silly and fun.  Second, this dataset is rich with potential for achieving pedagogical goals, such as exploring the seemingly simple but actually challenging concept of a statistical tendency. 

I mentioned in post #35 (Statistics of illumination, part 4, here) that psychologist Keith Stanovich has called probabilistic reasoning “the Achilles heel of human cognition.”  Data on Scrabble points in students’ names can help students to confront misunderstandings about this topic.  The research question to be investigated is: Do people with longer names have more Scrabble points?  The answer is yes, as long as we are careful to regard this as a statistical tendency and not a hard-and-fast rule.  What does this mean?  We’ll explore that question in this post.  As always, questions for posing to students appear in italics.

---

Here are the Scrabble point values of the 26 letters:

Just to make sure that we’re all clear: Shakespeare has 11 letters and 20 Scrabble points (1 + 4 + 1 + 5 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 20) in his name.  Juliet has 6 letters and 13 points, and Romeo has 5 letters and 7 points*.  Among these three names, a name with more letters than another always has more Scrabble points.  So far this is a rule and not just a tendency.  But one need not look far to find an exception to this rule: Romeo’s friend Mercutio has 8 letters but only 12 points, so his name has more letters but fewer points than Juliet’s.

* This website (here) is helpful for speeding up these calculations.

Because longer names do tend to produce more points than shorter names, I propose examining the ratio of a name’s points to letters as a measure of the name’s Scrabble-strength.  These ratios are approximately 1.818 for Shakespeare, 2.167 for Juliet, 1.400 for Romeo, and 1.500 for Mercutio.  By this measure, Juliet has the Scrabble-strongest name and Romeo the least.

---

For the purpose of this post, I will use the names of the fifty states in the U.S. to illustrate the kinds of questions that can be asked and analyses that can be performed.  Before I show you the data: Make a guess for the state with the most letters, the state with the most points, and the state with the largest ratio.  Are your guesses made?  Ready for the answers?  Here’s the list of states, along with region of the country, number of words in the name, number of letters, number of Scrabble points, and ratio of points to letters:

Which states win bragging rights?  As indicated in bold in the table, Massachusetts, North Carolina, and South Carolina tie for the most letters with 13.  New Hampshire takes first place in number of Scrabble points with 25.  In the most coveted ratio category, the winner is Kentucky with 2.625 points per letter.

Now let’s return to the original question: Do states with more letters tend to have more points?  But first we can ask students a more basic question: What kind of graph would you produce to investigate this question?  Because both variables are numerical, we can examine a scatterplot of points versus letters:

Does this graph reveal a tendency for states with more letters to have more points?  How can you tell?  Yes, this graph displays a positive association between points and letters.  For example, states with 10 or more letters all have 15 or more points, whereas states with 6 or fewer letters all have 12 or fewer points.

What statistic could we calculate to quantify this tendency?  Make an educated guess for its value with these data.  Again because these are both numerical variables, we can calculate the correlation coefficient between points and letters.  Its value turns out to be 0.735, indicating a fairly strong, positive association.

Can you identify a pair of states for which the state with more letters has fewer points?  Indicate one such pair of states on the graph.  Many pairs of states buck the overall trend in this way.  One example is that Kentucky has fewer letters (8 vs. 9) but more points (21 vs. 15) than California, as shown here:

Another way to think about a statistical tendency is: Suppose that we select two of the fifty states at random.  Make an educated guess for the probability that the state with more letters also has more points.  This is equivalent to asking: Among all pairs of states, in what percentage does the state with more letters also have more points?  There are 50×49/2 = 1225 pairs of states.  I wrote a small program in R to analyze these 1225 pairs.  It turns out that 161 of the pairs have the same number of letters or the same number of points.  Of the remaining 1064 pairs, 802 satisfy the overall tendency (the state with more letters also has more points), and 262 run counter to that tendency.  So, the probabilities for a randomly selected pair of states are 802/1225 ≈ 0.655 that the state with more letters also has more points, 262/1225 ≈ 0.214 that the state with more letters has fewer points, and 161/1225 ≈ 0.131 that the states have the same number of letters or points.  If we restrict our attention to the pairs of states without ties, the probability is 802/1064 ≈ 0.754 that the state with more letters also has more points.  To simplify: The overall probability is about two-thirds that the state with more letters has more points, and this increases to three-fourths if we eliminate ties.

The following graph displays the least squares regression line for predicting number of points from number of letters:

How many points would this line predict for Puerto Rico, if it were to become a state?  Puerto Rico has 10 letters, so the line would predict 1.611 + 1.460 × 10 = 16.211 points.  Assess the accuracy of this prediction.  Puerto Rico actually has 14 Scrabble points, so the prediction overestimates by 2.211 points, which is an overestimate of about 15.8%.  Repeat for Guam.  Guam has 4 letters, so the line would predict 1.611 + 1.460 × 4 = 7.451 points, compared to 7 actual points for Guam.  This is an overestimate of only 0.451 points, for a percentage error of just 6.4%.

---

We can also use these data to look for a statistical tendency in comparing two groups.  Do you expect that states with two words in their name will tend to have more Scrabble points than states with one-word names?

Before we investigate this question, here’s a more basic one: What kind of graph can we use to answer these questions?  Most students recognize that this question involves comparing two groups on a numerical response, so we can use comparative dotplots or boxplots.  Consider these graphs:

Do these graphs reveal that two-word states tend to have more points than one-word states?  Yes, absolutely.  From the boxplots, we see that every value in the five-number summary of points is higher for the two-word states than the one-word states.  In particular, the median number of points is 19 for the two-word states, 11.5 for the one-word states.  The dotplots also reveal that every two-word state has at least 16 points, but only 10 of 40 one-word states have 16 or more points. 

Can you identify a pair of states that do not satisfy the overall tendency?  Certainly, there are many such pairs.  The most extreme example is that (one-word) Kentucky has 21 points and (two-word) Rhode Island has 16 points.  I wrote some R code to analyze the 40×10 = 400 pairs of states (with a one-word and a two-word state) and found that 305 follow the overall tendency (meaning that the two-word state has more points than the one-word state), 68 run counter to the tendency, and 27 have a tie for number of points.

Could we incorporate information on number of words in the state’s name into the scatterplot of points versus letters?  If so, how?  What do you expect to see?  Yes, here is a coded scatterplot, with one-word states represented by blue circles and two-word states by red squares:

What does this graph reveal?  As expected, the two-word states appear in the top right part of the graph, indicating that they tend to have more letters and more points than one-word states.  Also, perhaps surprisingly, the association between points and letters is much weaker among the two-word states than the one-word states.

---

Now let’s bring the ratio (points to letters) variable into the analysis.  Which group – one-word states or two-word states – do you expect to have larger ratio values, on average?  Do you expect the difference between the groups to be substantial or small?  Ready to see the graphs?  Here you go:

Compare and contrast the distributions of ratio values between these groups.  The two-word states have slightly larger ratios, on average, than one-word states.  The medians are approximately 1.73 and 1.57 for the two-word and one-word states, respectively.  The two-word states also have more variability in ratio values than one-word states.  Both distributions appear to be slightly skewed to the right, more so for the two-word states.  The one-word states have two outliers on the high end of the ratio values – Kentucky (2.625 points per letter) and Texas (2.400 points per letter).

Now: What kind of relationship (if any) do you expect to see in a scatterplot of ratio versus letters?  How about in a scatterplot of ratio versus points?  Ready to find out?  Here are the graphs:

Describe what these graphs reveal.  Also make educated guesses for the values of the two correlation coefficients.  As expected, we see that the ratio is positively associated with number of points.  But the association is slightly negative with number of letters.  It turns out that correlation coefficients are 0.554 between ratio and points, -0.142 between ratio and letters.

Which variable – points or letters – would be more helpful for predicting ratio?  Determine the equation of this least squares line.  Also calculate and interpret the value of r-squared.  Number of points will clearly be more helpful for predicting ratio than number of letters.  The equation of the least squares line turns out to be: predicted ratio = 1.034 + 0.04674 × points.  The value of r-squared is 30.7%, indicating that 30.7% of the variability in states’ ratios is explained by knowing their number of points.  This value is perhaps surprisingly small, considering that number of points is used directly in the calculation of ratio.

Do you think the regression model would be substantially improved by adding number of letters, as well as number of points, to the predictors of ratio?  Some students think that the answer is clearly yes, because number of letters is included in the calculation of ratio, just as number of points is included.  Other students believe that the answer is clearly no, because the scatterplot reveals a very weak association (correlation -0.142) between ratio and letters.  Software tells us that the regression model with both predictors is: predicted ratio = 1.6723 + 0.12095 × points – 0.20029 × letters.  It makes sense that the coefficient is positive for number of points and negative for number of letters.  The value of r-squared for this regression model is 96.4%, dramatically greater than the value of 30.7% based only on number of points as a single predictor.  The two predictors together do much better at predicting a state’s ratio value than the sum of their usefulness as individual predictors.

---

Some students might ask themselves: Hold on, we can calculate a state’s ratio exactly from its number of points and number of letters, so why is r-squared not 100%?  The answer is that multiple regression incorporates variables in the model additively, whereas the calculation of ratio involves dividing points by letters.

Can we find a clever work-around that uses multiple regression to predict ratio from points and letters exactly, with an r-squared value of 100%?  Yes, we can.  The key is to transform all three variables by taking logarithms.  Here are scatterplots of the transformed data:

What do these graphs reveal?  We see a moderate positive association between log(ratio) and log(points), and there’s very little association between log(ratio) and log(letters).  These graphs provide no hint of what the multiple regression model will reveal.

The multiple regression model with these transformed variables turns out to be: log(ratio) = log(points) – log(letters).  The value of r-squared with this model is 100%!  What happens when you back-transform this equation to get rid of the logs*?  The right-hand side of the equation can be expressed as: log(points/letters).  Then exponentiating both sides of the equation produces what we knew it would: ratio = points/letters.

* How about that: a chance to work with properties of logarithms!

---

Asking your students to analyze data from their own names is more fun than analyzing states’ names.  Let me show you some results from data on my colleagues rather than students.  The following graph comes from data on the 33 faculty members listed on the faculty directory webpage (here) for the Statistics Department at Cal Poly – San Luis Obispo in the Winter quarter of 2020:

The graph reveals who wins bragging rights: Maddie Schroth-Glanz has the most letters (18) and Scrabble points (40) in her name, while Jimmy Doi has the largest ratio of points to letters (23/8 = 2.875 points per letter)*.  The smallest values were proudly achieved by Soma Roy for the fewest letters (7) and Dennis Sun for the fewest points (10) and smallest ratio (1.111)**.

* I used names as they appeared on the faculty directory webpage.  I realize that using James instead of Jimmy, or Madeleine instead of Maddie, would have changed the data.

** Where is my name?  I have slightly more letters than average (12, average 11.4) but many fewer points than average (14, average 21.4).  Needless to say, this makes my points-to-letters ratio one of the smallest among my colleagues (1.167, third smallest of 33 names).

Again we see a statistical tendency here, as names with more letters tend to have more points.  But a longer name does not guarantee more points, which is what makes this a tendency rather than a rule.   Among the 33×32/2 = 528 pairs of names, 327 follow the tendency and 127 run counter to it, with 74 ties.

The regression line for predicting points from letters is also given in the graph, along with the r-squared value of 41.0%.  The line is a bit steeper than with the states’ names (slope 1.773 points per letter for faculty, compared to 1.460 points per letter for the states).  The value of r-squared is smaller for the faculty than for the states: 41.0% versus 54.1%.

Analyzing people’s names provides an opportunity to analyze paired data.  The following graph displays Scrabble points of last names versus first names for these faculty, along with a 45 degree line:

What tendency is revealed by most of the names falling above the 45 degree line? A slight tendency for more points in a faculty member’s last name than first name.

---

Depending on your course goals and student audience, you could also ask students to do some coding associated with data on Scrabble points.  Such an activity could include scraping names from a webpage, and it might also use a mapping of letters-to-points for games other than Scrabble, such as Words with Friends. I recently attended an inspiring presentation by Paul Myers (9 letters, 16 points, 1.778 ratio), who asks high school students in a data science* class to write code (in both Excel and R) for calculating numbers of letters and Scrabble points in names. 

* Have you noticed that data science has more letters, more Scrabble points, and a larger points-to-letters ratio than statistics?

Recommendation #3 of the GAISE report (here) is: Integrate real data with a context and purpose.  These data on Scrabble points do not have much purpose, other than being fun, but they do provide opportunities to explore statistical concepts.  Chief among these is the concept of a statistical tendency, which is quite fundamental but can prove elusive to many students.

Perhaps if Shakespeare had been a (far-ahead-of-his-time) statistician or data scientist, he might have asked: What tends to be in a name?

P.S. An Excel file with the data on states’ names can be found below.  Graphs in this post were produced with Minitab statistical software.

P.P.S. As so many teachers prepare to teach remotely in the coming weeks, I regret that I have no experience with online teaching and so have no advice to offer*.  Because I am on leave this academic year, I am not embarking on this foray into a brave new world alongside so many of you.  I wish you and your students well in these challenging circumstances.

* Other than: Ask good questions! 🙂

P.P.P.S. I’m a big fan of simulations*.  I highly recommend this article (here) by Harry Stevens, which shows simulations of virus spread under four conditions, illustrating the potential impact of social distancing.

* See posts #12, #13, and #27 (here, here, and here) on simulation-based inference, post #14 (here) on interpreting confidence level, and posts #23 and #24 (here and here) for simulation analyses of a probability problem.